Link (geometry)
In geometry, the link of a vertex of a 2-dimensional simplicial complex is a graph that encodes information about the local structure of the complex at the vertex.
It is a graph-theoretic analog to a sphere centered at a point.
Example
The link of a vertex of a tetrahedron is a triangle – the three vertices of the link corresponds to the three edges incident to the vertex, and the three edges of the link correspond to the faces incident to the vertex. In this example, the link can be visualized by cutting off the vertex with a plane; formally, intersecting the tetrahedron with a plane near the vertex – the resulting cross-section is the link.
Definition
Let 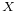 be a simplicial complex. The link
be a simplicial complex. The link 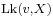 of a vertex
of a vertex 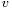 of
of 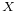 is the graph constructed as follows. The vertices of
is the graph constructed as follows. The vertices of 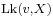 correspond to edges of
correspond to edges of 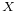 which are incident to
which are incident to 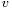 . Two such edges are adjacent in
. Two such edges are adjacent in 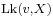 if they are incident to a common 2-cells at
if they are incident to a common 2-cells at 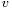 . In general, for an abstract simplicial complex and a face
. In general, for an abstract simplicial complex and a face 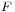 of
of 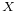 , denoted
, denoted 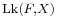 is the set of faces
is the set of faces 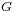 such that G
such that G  F =
F = 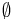 and G
and G 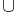 F
F 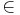 X. Because
X. Because  is simplicial, there is a set isomorphism between
is simplicial, there is a set isomorphism between 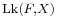 and
and 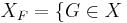 such that F
such that F 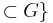 .
.
The graph 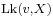 is often given the topology of a ball of small radius centred at
is often given the topology of a ball of small radius centred at 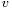 .
.
References
- Bridson, Martin; Haefliger, André (1999), Metric spaces of non-positive curvature, Springer, ISBN 3-540-64324-9